회귀 분석

누구에게나 “이거다!” 하는 순간이 온다.
중요한 것은 그 순간에 어떻게 이어나갈 것인지 생각하는 것이다.

---

y = Wx + b

데이터 포인트들의 집합 x와 예측 값 y는 행렬-벡터 곱의 공식이 됩니다.

x와 y의 관계가 대략 선형적이다.

• 수학에서 나타내는 1차식 , 1차 함수로 개의 직선으로 그래프가 표현된다. 1개의 일정한 기울기를 가지고 기울기의 변화가 없는 것

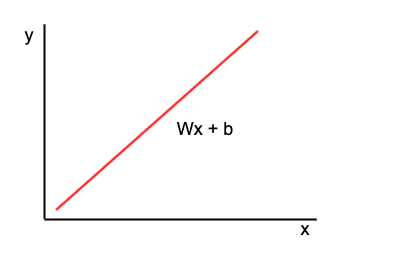
1차 선형 방정식으로 그래프 상에서 선형적으로 증가한다.

• 항목 정의
  • y는 우리가 원하는 값
  • x는 입력데이터
    • w : 가중치 ( 기울기 )
    • b : 편향

y에 대한 x를 정의 할 때 x의 값에 대한 w, b를 구하는 것이 중요

주어진 데이터로 어떤 함수를 만들어 낸 후, 이 함수가 얼마나 정확한지 피팅하는 작업, 통계적 예측에 이용, 가정을 통해 회귀모형을 만들고 이 회귀모형의 적합도를 검정을 통해 확인하는 과정이 필요

Python을 이용한 회귀 분석

from sklearn.linear_model import LinearRegression
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

df = pd.read_csv("heights.csv")
df.head()

X = df["weight"]
y = df["height"]
#plt.plot(X, y, 'o')
#plt.show()

line_fitter = LinearRegression()
line_fitter.fit(X.values.reshape(-1,1), y)

print(line_fitter.predict([[70]]))

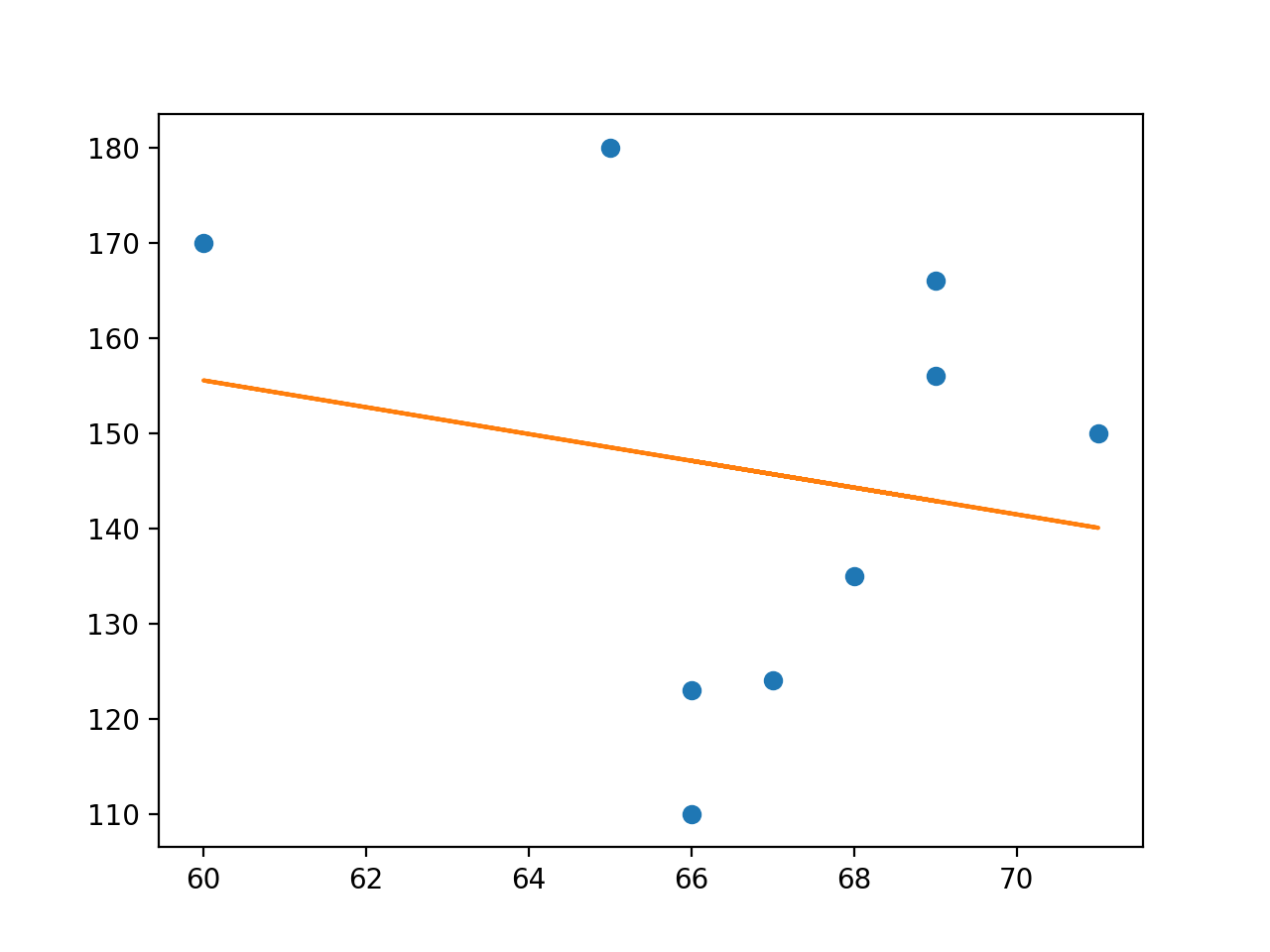
plt.plot(X, y, 'o')
plt.plot(X,line_fitter.predict(X.values.reshape(-1,1)))
plt.show()

• 그래프 결과