데이터 분석 2일차 - 선형회귀 분석
Higher Hope.
데이터 분석 - 선형 회귀 분석 2일차
단순 선형 회귀는 반응 변수와 설명 변수 간에 선형 관계가 존재한다고 가정하고 초평면이라고 불리는 선형 평면을 이용해 관계를 모델링한다. 초평면은 자신을 포함하고 있는 차원보다 한 차원 낮은 부분 공간이다. 단순 선형회귀에서는 반응 함수를 위한 차원 하나와 설명 변수의 차원 하나를 더해 모두 2차원이 있다. 따라서 선형 회귀 초평면은 1차원이 되고 1차원 초평면은 선이다.
수학에서, 초평면(超平面, 영어: hyperplane)은 3차원 공간 속의 평면을 일반화하여 얻는 개념이다.
컴퓨터에서 벡터는 화상의 표현 요소로서의 방향을 지닌 선. 선그림.
인과 관계 : 만약 변수 X가 다른 변수 Y에 영향을 주는 관계에 있다면 통계에서는 이를 “인과관계”가 있다고 합니다.
설명 변수 : 이때 각 변수 중 영향을 주는 변수를 독립변수라고 하는데요. 독립변수는 다른 말로설명변수(explanatory variable) 라고 합니다.
반응 변수 : 그리고 영향을 받는 변수를 종속변수라고 하는데 이 종속변수를 다른 말로 반응변수(response variable) 라고 하구요.
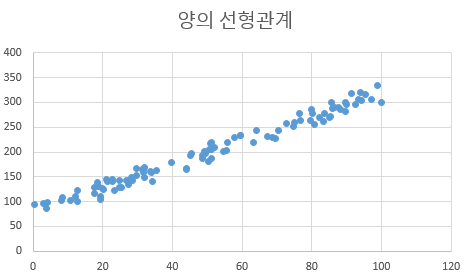
선형 관계 : 선형관계는 두 데이터 값사이에 직선식의 형태가 있으면 선형관계가 있다고 한다. 선형관계는 영어로 Linear Relationship 이므로 직선과 어떤 연관이 있다는 것을 알 수 있다.아래의 의 산포도와 같이 데이터가 분포된 형태가 마치Y = aX+B [여기서 a는 양의 정수]의 형태로 나타날 때 독립변수와 종속변수에는 양(+)의 선형관계(Positive linear relationship)가 존재한다고 한다.
LinearRegression 클래스는 예측기이다. 예측기는 관찰 데이터로 부터 값을 예측한다.
scikit-learn의 모든 예측기에는 fit 와 predict가 구현되어 있다.
-
fit은 모델의 매개변수를 학습하기 위해서 사용된다.
-
predict는 학습된 매개변수를 사용해 주어진 설명 변수에 해당하는 반응 변수 값을 예측하기 위해 사용한다.

Linear Regression의 fit 메소드는 단순 선형 회귀를 위한 다음과 같은 모델의 매개변수를 학습한다.
y = α + βx
위의 공식에서 y는 반응 변수의 예측 값이다. 이 예제에서 예측 값은 피자 가격이 된다. x는 설명번수다. 절편항 α와 계수 β는 학습 알고리즘을 통해 학습하게 되는 모델의 매개변수이다.
from sklearn.linear_model import LinearRegression
import numpy as np
# X는 훈련데이터의 특징이고, 여기서는 피자의 지름이다.
# scikit-learn은 특징 벡터 이름을 X로 사용한다.
# 대문자는 행렬을 의미하고 소문자는 벡터를 의미한다.
X = np.array([[6], [8], [10], [14], [18]]).reshape(-1, 1)
y = [ 7, 9, 13, 17.5, 18 ] # y 피자가격을 나타내는 벡터이다.
model = LinearRegression() # 예측기 생성 - 선형회귀
model.fit(X, y) # 훈련 데이터에 모델 적합화
# 임의의 변수를 입력하여 계산된 선형 그래프 상에서 피자의 가격을 예측
test_pizza = np.array([[12]])
predicted_price = model.predict(test_pizza)[0]
print('A 12" pizza should code : $%.2f' % predicted_price)
단순 선형 회귀에서 모델을 최적 최적합화 하는 매개변수 값을 훈련 데이터로부터 학습하는 것을 최소 자승법 또는 선형 최소 자승법이라 한다.
비용함수는 손실함수라고도 불리며, 모델의 오차를 정의하고 측정하기 위해 사용된다. 모델에 의해 예측된 가격과 훈련 데이터에서 관측된 가격과의 차이를 잔차 또는 훈련 오차라고도 한다.
나중에 별도의 테스트 데이터를 상대로 모델을 평가하게 된다. 예측 값과 테스트 데이터의 관찰 값 사이의 차이를 예측 오차 또는 테스트 오차라 한다.
잔차의 합을 최소화하면 최적의 피자 가격 예측기를 만들 수 있다. 즉, 모델이 예측하는 반응 변수가 모든 훈련 예시의 관측 값이 가까워지면 모델이 적합화됐다고 할 수 있다. 이러한 모델의 적합화 척도를 잔차 제곱의 합 비용 함수라고 한다. 형식을 갖춰 설명하자면 이 함수는 모델의 적합도를 평가하기 위해서 모든 훈련 예시의 잔차를 제곱한 값을 더한다.
Numpy - Reshape
reshape함수는 np.reshape(변경할 배열, 차원) 또는 배열.reshape(차원)으로 사용 할 수 있으며, 현재의 배열의 차원(1차원,2차원,3차원)을 변경하여 행렬을 반환하거나 하는 경우에 많이 이용되는 함수이다.
- numpy : reshape
import numpy as np
a = [1,2,3,4,5,6]
b = np.reshape(a,(2,3))
c = np.reshape(a,(3,2))
print(b)
print('\n')
print(c)
- result
D:\GIT\sample\sample\python\python_deeplearning\venv\Scripts\python.exe D:/GIT/sample/sample/python/python_deeplearning/dataanalysis_20210818.py
[[1 2 3]
[4 5 6]]
[[1 2]
[3 4]
[5 6]]
Process finished with exit code 0
reshape를 활용하는 경우를 보다 보면 입력인수로 -1이 들어간 경우가 종종 있다. reshape()의 ‘-1’이 의미하는 바는, 변경된 배열의 ‘-1’ 위치의 차원은 “원래 배열의 길이와 남은 차원으로 부터 추정”이 된다는 뜻이다. 즉, 행(row)의 위치에 -1을 넣고 열의 값을 지정해주면 변환될 배열의 행의 수는 알아서 지정이 된다는 소리이다.
최소 자승법
모델의 파라미터를 구하기 위한 대표적인 방법 중 하나로서 모델과 데이터와의 redidual^2의 합 또는 평균을 최소화 하도록 파라미터를 결정하는 방법이다.
Residual 은 어떤 데이터가 추정된 모델로부터 얼마나 떨어진 값인가를 나타내는 용어이다. 어쨌든, 관측된 데이터를 보고 어찌 어찌 계산을 해서 구한 모델이 f(x) = a1x + b1 라고 해보자. 원래 간측된 데이터 분포가 완벽한 직선이 아니라면 어떻게 직선(모델)을 구하더라도 몇몇 데이터를은 오차를 갖게 된다. 이 오차를 residual이라고 부른다. 즉, 데이터( xi, yi)의 residual은 ri = yi - f(xi)가 된다. 여기서 yi는 관측된 값이고 f(xi)는 추정된 모델에 따른 값이다.
최소 자승법의 계산 방식
최소 자승법은 어떤 기준을 가지고 모델의 파라미터를 구하는가를 말해줄 뿐 실제로 이걸 어떻게 계산하는가는 별개의 문제이다. 실제 계산을 못한다면 활용하기 힘든 만큼 최소 자승법을 어떻게 계산하느냐도 매우 중요하다.
- 대수적 방법
먼저, 대수적 장법은 위의 모델 추정 문제를 행렬식 형태로 표현한 후 선형 대수학을 적용하는 방법이다. 직선의 f(x) = ax + b 추정 문제는 결국 다음 식들은 만족하는 a, b를 찾는 것이다.
ax1 + b = y1
ax2 + b = y2
.
.
.
axn + b = yn
이를 행렬 백터로 표현할 수 있습니다.
AX = B