순환(재귀)에 대해서
삶이라는 것이 쉽지가 않다. 늘 그렇다. 답을 찾지도 못하고 그냥 가만히 있는 수 밖에
어떤 알고리즘이나 함수가 자기 자신을 호출하여 문제를 해결하는 프로그래밍 기법이다.
순환의 예 : 순환은 본질적으로 순환적인 문제나 그러한 자료구조를 다루는 프로그램에 적합하다.
int factorial(int n){
if( n <= 1) return(1);
else return (n*factorial(n-1))
}
// 위의 코드를 아래의 Factorial 기준대로 정의하는 방법
/*
factorial(3) = 3 * factorial(2);
= 3 * 2 * factorial(1);
= 3 * 2 * 1
= 3 * 2
= 6
*/
순환의 동작원리
순환을 이해하기 위하여 먼저 함수 호출의 과정을 살펴보면, 프로그래밍 언어에서 하나의 함수가 자기 자신을 다시 호출하는 것은 다름 함수를 호출하는 것과 동일하다. 즉 복귀 주소가 시스템 스택에 저장되고 호출되는 함수를 위한 매개변수와 지역 변수를 스택으로부터 할당 받는다. 이러한 함수를 위한 시스템 스택에서의 공간을 활성 레코드라 한다. 이러한 준비가 끝나면 호출된 함수의 시작위치로 점프하여 수행을 시작한다. 만약 호출한 함수가 끝나게 되면 시스템 스택에서 복귀주소를 추출하여 호출한 함수로 되돌아가게 된다.
순환 알고리즘의 구조
int factorial( int n )
{
if ( n <= 1 ) return (1);
return ( n * factorial(n-1));
}
기본 연산의 횟수가 다향식으로 표현되었을 경우 다항식의 최고차항만을 남기고 다른 항들과 상수항을 버리는 것이다. 최고 차항의 계수도 버리고 단치 최고차항의 차수만을 이용한다.
순환 <-> 반복
반복이란 for나 while 등의 반복구조로 되풀이 하는 방법이다. 반복을 제어하는 변수를 사용하여 일정횟수 동안 반복 시킬수도 있고 어떤 조건이 만족될 때까지 반복시킬 수도 있다. 반복은 간단명료하여 효율적으로 되풀이를 구현하는 방법이다. 반면에 때로는 반복을 사용하게 되면 지나치게 복잡해지는 문제들도 존재한다. 이런 경우에는 순환이 좋은 해결책이 될 수 있다. 순환은 주어진 문제를 해결하기 위하여 자신을 다시 호출하여 수행하는 방식이다. 순환은 본질적으로 순환적인 문제나 그러한 자료구조를 다루는 프로그램에 적합하다. 문제의 크기가 순환이 진행될수록 작아지는 것에 유의해야 한다. 기본적으로 반복과 순환은 문제 해결 능력이 같으며 많은 경우에 순환 알고리즘을 반복 버전으로, 반복 알고리즘을 순환 버전으로 바꾸어 쓸 수 있다. 특히 순환 호출이 끝에서 이루어지는 순환을 꼬리 순환이라고 하는데, 이를 반복 알고리즘으로 쉽게 바꾸어 쓸 수 있다.
순환의 원리
분할 정복 : 주어진 문제를 더 작은 동일한 문제들로 분해하여 해결하는 방법을 분할 정복이라 한다. 순환은 알고리즘 정의가 순환적으로 되어 있는 경우에 유리한 방법이다. 예를 들어 팩토리얼 함수 계산, 피보나치 수열, 이항계수 계산, 이진 트리 알고리즘, 이진 탐색, 하노이 탑 문제들은 순환 알고리즘을 쓰는 것이 자연스러운 알고리즘이다.
순환 알고리즘의 성능
순환 알고리즘과 반복 알고리즘의 시간 복잡도는 같지만 순환 호출의 경우 여분의 기억공간이 더 필요하고 또한 함수를 호출하기 위해서는, 함수의 매개변수들을 스택에 저장하는 것과 같은 사전 작업이 상당히 필요하다. 따라서 수행시간도 더 걸린다. 결론적으로 순환 알고리즘은 이해하기 쉽다는 것과 쉽게 프로그램 할 수 있다는 장점이 있는 대신 수행 시간과 기억 공간의 사용에 있어서는 비효율적인 경우가 많다.
- 거듭제곱 값 계산
// 반복에 의한 방식
double slow_power(double x, int n){
int i;
double result = 1.0;
for( i = 0; i < n; i ++ ){
return = result * x;
return (result);
}
}
// 순환에 의한 방식
// 한번의 호출 할 때마다 문제의 크기는 약 절반으로 줄어든다.
power(x , n) :
if n == 0
then return 1;
else if n이 짝수
then return power(x^2, n/2);
else if n이 홀수
then return x * power(x^2, (n-1)/2);
// 순환적인 거듭 제곱 계산
// 순환을 사용하게 되면 단순하게 작성이 가능하며 가독성이 높아진다. 그러나 똑같은 계산을 몇번씩 반복한다면 아주 단순한 경우라 할지라도
// 계산 시간이 엄청나게 길어질 수 있다.
double power(double x, int n ){
if ( n == 0) return 1;
else if ( (n%2) == 0)
return power(x*X, n/2 )
else return x * power(x*x, (n-1)/2);
}
피보나치 수열
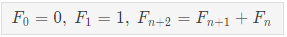
- 피보나치 수열은 이탈리아 수학자가 발견한 수열로서 한 쌍의 토끼가 번식하는 상황을 수열로 만든 것이다.
// 순환적인 피보나치 수열 계산
int fib(int n){
if ( n == 0) return 0;
if ( n == 1) return 1;
return ( fib(n-1) + fib(n-2));
}
위의 코드는 단순하고 이해하기 쉽지만 굉장히 비효율적인 코드이다. fib(6)을 구하기 위해서 fib() 함수가 25번이나 호출되는 것에 유의해야 한다. 근본적인 이유는 중간에 계산되었던 값을 기억하지 않고 다시 계산하기 때문이다. T(n) = T(n-1) + T(n-2) + C 의 순환적인 수식을 이용하면 시간 복잡도 O(2^n)이 도출된다. 이것은 O(2^n)의 복잡도 패턴이라 할 수 있다. 피보나치 수열을 계산하는데 순환을 사용하는 것이 아닌 반복을 사용하게 되면 제일 좋은 결과를 얻을 수 있었다.
int fib_iter(int n){
if ( n == 0 ) return 0;
if ( n == 1 ) return 1;
int pp = 0;
int p = 1;
int result = 0;
for( int i = 2 ; i < n; i ++){
result = p + pp;
pp = p;
p = result;
}
return result
}
하노이탑
순환의 사용에 가장 적합한 예제가 바로 하노이 탑 문제이다.
// 막대 from에 쌓여있는 n개의 원판을 막대 tmp를 사용하여 막대 to로 옮긴다.
void hanoi_tower(int n, char from, char tmp, char to ){
if ( n == 1) {
from에 있는 한 개의 원판을 to로 옮긴다.
} else {
1. from의 맨 밑의 원판을 제외한 나머지 원판을 tmp로 옮긴다.
2. from에 있는 한 개의 원판을 to로 옮긴다.
3. tmp의 원판들을 to로 옮긴다.
}
}
// 코드 예제
#include <stdio.h>
void hanoi_tower( int n , char from, char tmp, char to ){
if ( n == 1) printf("원판 1을 %C에서 %c으로 옮긴다. \n" , from, to );
else {
hanoi_tower( n - 1, from, to tmp );
printf("원판 %d 을 %C에서 %c으로 옮긴다. \n" , from, to );
hanoi_tower( n - 1, tmp, from, to );
}
}
int main(void){
hanoi_tower( 4, 'A' , 'B' , 'C');
return 0;
}
// 순환 호출이 맨끝에서 이루어지는 형태의 순환으로, 꼬리 순환의 경우, 알고리즘은 쉽게 반복적인 형태로 변환이 가능하다.
return n*factorial(n - 1);
// 머리 순환(head recursion)의 경우나 방금 살펴본 하노이 탑의 문제 처럼 여러 군데에서 자기 자신을 호출하는 경우는 쉽게 반복적인 코드로 바꿀 수 없다.
return factorial(n - 1)*n;