빅오 표기법에 대하여
다들 사는 데 이유가 있겠지, 나도 살아야할 이유가 있겠지.
일반적으로 입력의 개수 n과 시간 복잡도 함수 T(n)의 관계는 상당히 복잡할 수 있다. 하지만 자료가 많은 경우에는 차수가 가장 큰 항이 가장 영향을 크게 미치고 다른 항들은 상대적으로 무시될 수있다. 예를 들어
T(n) = n^3 + n + 1
위의 항에서 n이 10000일 때, n^3의 값이 전체의 값을 주도한다는 것을 알 수 있다. 따라서 시간 복잡도 함수에서 차수가 가장 큰 항만을 고려하면 충분하다. 시간 복잡도 함수 에서 중요한 것은 n이 증가하였을 때, 연산의 총횟수가 n에 비례하여 증가하는지, n^2에 비례하여 증가하는지, 아니면 다른 추세를 가지는지가 더 중요하다. 정확한 연산의 개수 보다 알고리즘의 일반적인 증가 추세가 더 중요하다. 2n과 4n + 1의 차이는 n이 커지게 되면 미미하다고 할 수 있다. 따라서 시간 복잡도 함수에서 불필요한 정보를 제거하여 알고리즘 분석을 더욱 쉽게 할 목적으로 시간복잡도를 표시하는 방법을 빅오 표기법이라고 한다. 즉 알고리즘이 n에 비례하는 수행 시간을 가진다고 말하는 대신에 알고리즘 A의 시간 복잡도 합수가 O(n)이라고 한다.
빅오 표기법 정의
두 개의 함수 f(n)과 g(n)이 주어졌을 때 모든 n > n0에 대해여 |f(n)| <= c|g(n)|을 만족하는 2개의 상수 c와 n0가 존재하면 f(n)=O(g(n)) 이다.
빅오 표기법에서 중요한 것은 알고리즘의 일반적인 증가 추세가 중요하다는 것이다.
- 빅오 표기법 예제
f(n)=5이면 O(1)이다.
f(n)=2n+1이면 O(n)이다.
f(n)=3n^2+100이면 O(n^2)이다.
f(n)=5*2^n이면 O(n^2)이다.
f(n)=5*2^n+10n^2 + 100이면 O(2^n)이다.
f(n)=7n-3이면 O(n)
8n^2logn + 5n^2 + n = O(n^2logn)
기본 연산의 횟수가 다향식으로 표현되었을 경우 다항식의 최고차항만을 남기고 다른 항들과 상수항을 버리는 것이다. 최고 차항의 계수도 버리고 단치 최고차항의 차수만을 이용한다.
빅오표기법에 따른 표현방식
- O(1) : 상수형
- O(logn) : 로그형
- O(n) : 선형
- O(nlogn) : 선형 로그형
- O(n^2) : 2차형
- O(n^3) : 3차형
- O(2^n) : 지수형
- O(n!) : 팩토리얼형
위의 순서대로 알고리즘의 수행시간에 걸리는 순서도 같이 확인할 수 있다. 아래로 내려가면 갈수록 걸리는 시간이 커진다.
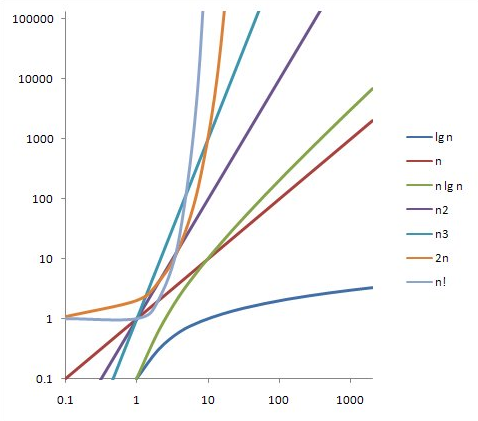
빅오 표기법 이외의 표기법들
- 빅오메가 표기법 : 어떤 함수의 하한을 표기하는 방법
- 빅세타 표기법 : 동일한 함수로 상한과 하한을 만들 수 있는 경우
표기법 중에 가장 정밀한 것은 빅세타 표기법이다.
똑같은 알고리즘도 주어지는 입력의 집합에 따라 다른 수행 시간을 보일 수 있다. 즉 특정한 자료 집합이 주어지면 다른 자료 집합보다 더 빨리 수행할 수 있다. 최악의 경우는 자료집합 중에서 알고리즘의 수행시간이 가장 오래 걸리는 경우이다. 최선의 경우는 수행시간이 가장 적은 경우이다. 평균적인 경우는 알고리즘의 모든 입력 고려하고 각 입력이 발생하는 확률을 고려하여 평균적인 수행시간이 의미한다.
우리가 구하려는 데이터의 자료구조에 따라 빅오 표기법의 복잡도가 상이해질 수 있는데, 아래의 코드를 보면
// 최선의 경우는 찾고자 하는 숫자가 배열의 맨 처음에 있는 경우이다. 따라서 빅오 표기법은 O(1)
// 최악의 경우는 찾고자 하는 숫자가 맨 마지막이 있는 경우이다. 따라서 빅오 표기법으로는 O(n)
int seq_search(int list[], int key ){
int i;
for ( i = 0; i< n ; i ++){
if(list[i] == key){
return i;
}
}
}
위의 코드가 의미하는 바는 상당히 중요하다. 왜냐하면 결국 시간복잡도의 최선의 경우를 구하는 것은 데이터를 구성하는 자료 구조가 얼마나 중요한지 알수 있다. 이 때문에 데이터를 추출하고, 정렬하여 우리가 원하는 자료구조를 만들어 이에 최선인 시간복잡도를 구하는 일이 무엇보다 중요하다.